27.
Математический пакет Maple — среда для решения
математических задач. Основы работы, команды. Построение графиков функций.
Решение дифференциальных уравнений. На персональном компьютере сегодня можно решать задачи
научно-технического характера, не прибегая к их кодированию на каком-нибудь
алгоритмическом языке (Бейсик, Паскаль, СИ). Использование интегрированных
программных систем автоматизации математических расчетов (Eureka, Maple, Mathematica, MatLab, MathCAD и др.) позволяют решать поставленные задачи на
входном языке, который максимально
приближен к естественному математическому языку. С каждой новой версией Maple добавляются новые математические пакеты расширения и
применения для решения задач. По изучению приемам работы и методики решения физических задач в системe Maple мы
отсылаем к книгам [6, 11]. Знакомство
с системой Maple. Интерфейс данной системы адаптирован
для работы пользователя, имеющего элементарные навыки работы с Windows-приложениями.
Под интерфейсом понимается не только легкое управление
системой, как с клавишного пульта, так и с помощью мыши, но и просто набор
необходимых символов, формул, текстовых комментариев с последующим запуском
документов (Worksheets) в реальном времени.
Запустив систему Maple из Windows, вы
увидите на экране окно (рис. 1.11). Над ним видна строка с основными элементами
интерфейса. Опции главного меню, содержащиеся в этой строке, легко изучить
самостоятельно через опцию Help; некоторые
из них очень похожи на стандартные опции, принятые в текстовых редакторах Windows.
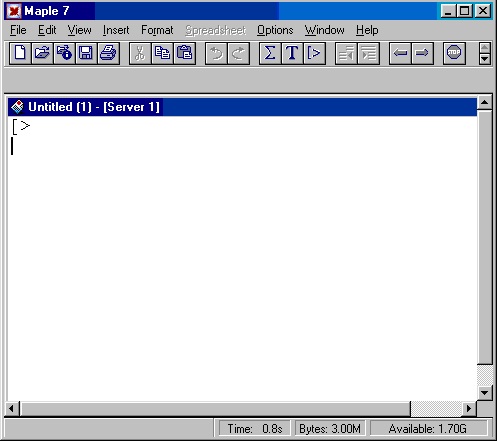
Рис.1.11
Остановимся на применении системы Maple для решения дифференциальных уравнений. Для решения
простых обыкновенных дифференциальных уравнений (ОДУ) и систем (ОДУ)
используется процедура пакета Maple dsolve,
которая в общем виде записывается как:
dsolve ( { ODE, nach
}, { funcs }, type solution).
Здесь ODE –
идентификатор, которому присваивается дифференциальное уравнение (система ОДУ)
или само ДУ;
nach –
начальные условия;
funcs –
определяемые функции;
type solution – опция, задающая метод аналитического или численного
решения. Этот параметр определяет тип используемого метода аналитического или
численного решения ОДУ. При задании этого параметра в виде:
·
еxplicit – выдает явное решение;
·
formal series –
решение в форме степенного многочлена;
·
series – решение в виде ряда с порядком, которое указывается
впереди функции dsolve в виде Order:=8;
·
integral transform –
решение на основе интегральных преобразований Лапласа, Фурье и др.;
·
numeric – решение в численном виде.
Если мы не указываем этот параметр, то система сама
выбирает предпочтительный метод решения по умолчанию.
Рассмотрим в краткой форме процесс решения
дифференциальных уравнений и моделирования физических задач в системе Maple [12, 28] на примере уравнения
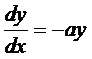 . .
Среда
допускает произвольную запись нахождения решения. Она может быть оформлена через
операторы присвоения, например
Ø ODE:=diff(y(x),x)=-a*y(x)
Ø Nach:=y(0)=5; (2)
Ø
dsolve({ODE,Nach},y(x));
или
уравнения, начальные значения, определяемые функции, используемый метод решения
записываются в одной строке, например
Ø
dsolve({diff(y(x),x)=-a*y(x),y(0)=5},y(x)); (3)
возможна также
их комбинация. Полученное решение может быть присвоено какому-либо оператору
Ø
F:=dsolve({diff(y(x),x)=-a*y(x),y(0)=5},y(x));
Построение
графика может быть проведена с помощью опции в виде
Ø
with(plots);
Ø
odeplot(F,[x, y(х)],0..200);
или использовать равнозначную запись
Ø
plots[odeplot](F,[x, y(х)],0..200);
Рекомендации при использовании системы Maple:
1) система различает заглавные и маленькие буквы;
2) необходимо строго соблюдать открытие и закрытие как
фигурных, так и круглых скобок;
3) Необходимо аккуратно следить за знаками двоеточие и
точка с запятой.
Пример 1. Движение небесного тела в
гравитационном поле
описывается системой уравнений 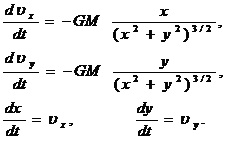
с начальными условия определенными двумя параметрами: начальной
скоростью и углом a.
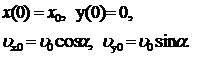
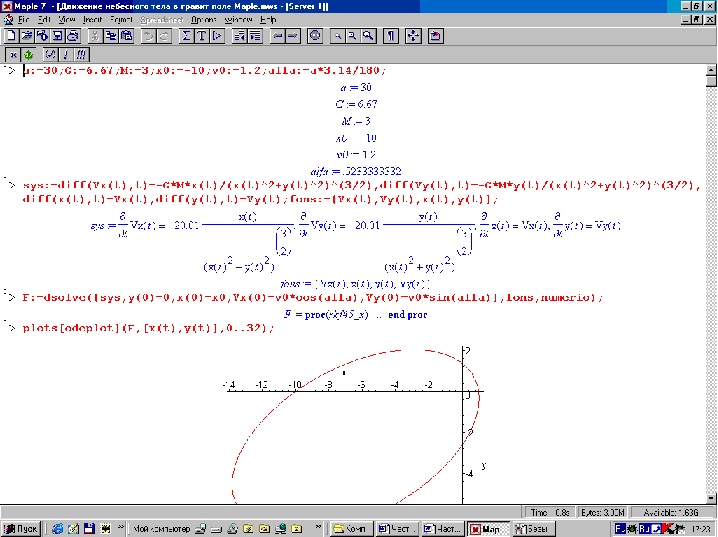
Ниже
приведены численные решения дифференциальных уравнений ( ). На график выведены траектории движения
небесного тела в зависимости от начальной скорости
> v0:=2;sys:=diff(Vx(t),t)=-G*M*x(t)/(x(t)^2+y(t)^2)^(3/2),
diff(Vy(t),t)=-G*M*y(t)/(x(t)^2+y(t)^2)^(3/2), diff(x(t),t)=Vx(t),
diff(y(t),t)=Vy(t):fons:={Vx(t),Vy(t),x(t),y(t)}:
F:=dsolve({sys,y(0)=0,x(0)=5,Vx(0)=v0*cos(alfa),
Vy(0)=v0*sin(alfa)},fons,numeric): plots[odeplot](F,[x(t),y(t)],0..200);
v0:=2
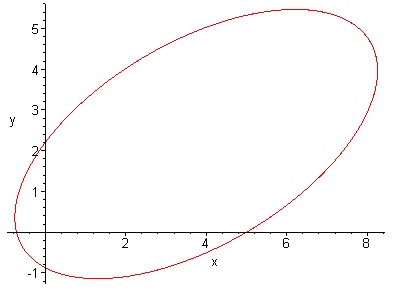
> v0:=3.5;sys:=diff(Vx(t),t)=-G*M*x(t)/(x(t)^2+y(t)^2)^(3/2),
diff(Vy(t),t)=-G*M*y(t)/(x(t)^2+y(t)^2)^(3/2), diff(x(t),t)=Vx(t),
diff(y(t),t)=Vy(t):fons:={Vx(t),Vy(t),x(t),y(t)}:
F:=dsolve({sys,y(0)=0,x(0)=x0,Vx(0)=v0*cos(alfa), Vy(0)=v0*sin(alfa)},fons,numeric):
plots[odeplot](F,[x(t),y(t)],0..30);
v0:=3.5
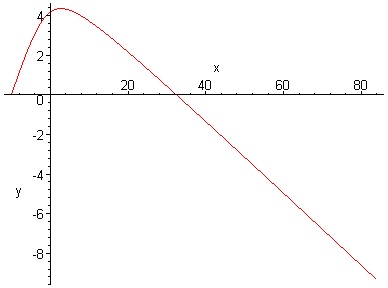
> v0:=0.005;sys:=diff(Vx(t),t)=-G*M*x(t)/(x(t)^2+y(t)^2)^(3/2),
diff(Vy(t),t)=-G*M*y(t)/(x(t)^2+y(t)^2)^(3/2),
diff(x(t),t)=Vx(t),diff(y(t),t)=Vy(t): fons:={Vx(t),Vy(t),x(t),y(t)}: F:=dsolve({sys,y(0)=0,x(0)=x0,Vx(0)=v0*cos(alfa),
Vy(0)=v0*sin(alfa)},fons,numeric): plots[odeplot](F,[x(t),y(t)],0..650);
v0:=.005
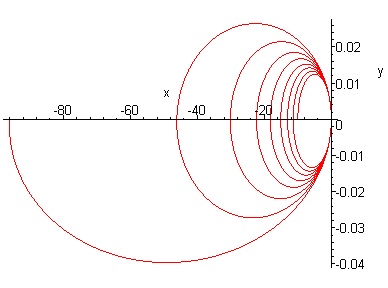
| 








